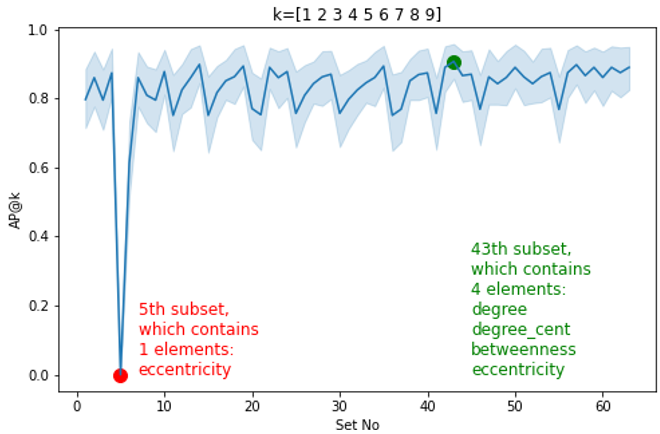
Combinatorial optimization

Combinatorial optimization as a major domain of CS

Combinatorial optimization is a field within computer science that focuses on finding the optimal solution among a finite set of possibilities. It involves solving complex problems by determining the best combination of variables to achieve an objective. Some examples of combinatorial optimization problems include:

  • Tiling problems: The tiling problem is a type of combinatorial problem that asks how to cover a given region with a given set of tiles, without any gaps or overlaps. The region and the tiles can have different shapes and sizes, and the tiles can be placed in different orientations. The tiling problem can have various applications, such as art, cryptography, geometry, and computer science. The tiling problem can also have different variations, such as counting the number of possible tilings, finding a specific tiling, or determining whether a tiling exists or not.

  • Time tabling: In this problem, the goal is to create an optimal schedule for activities, taking into consideration constraints such as available resources, time slots, and preferences. This is commonly used in school timetables, conference schedules, or employee shift planning.

  • Cutting and packing problems: These problems involve finding the most efficient way to cut or pack objects into specific shapes or containers. This is commonly used in logistics and manufacturing industries to optimize the use of space, minimize shipping costs, or maximize loading capacity.

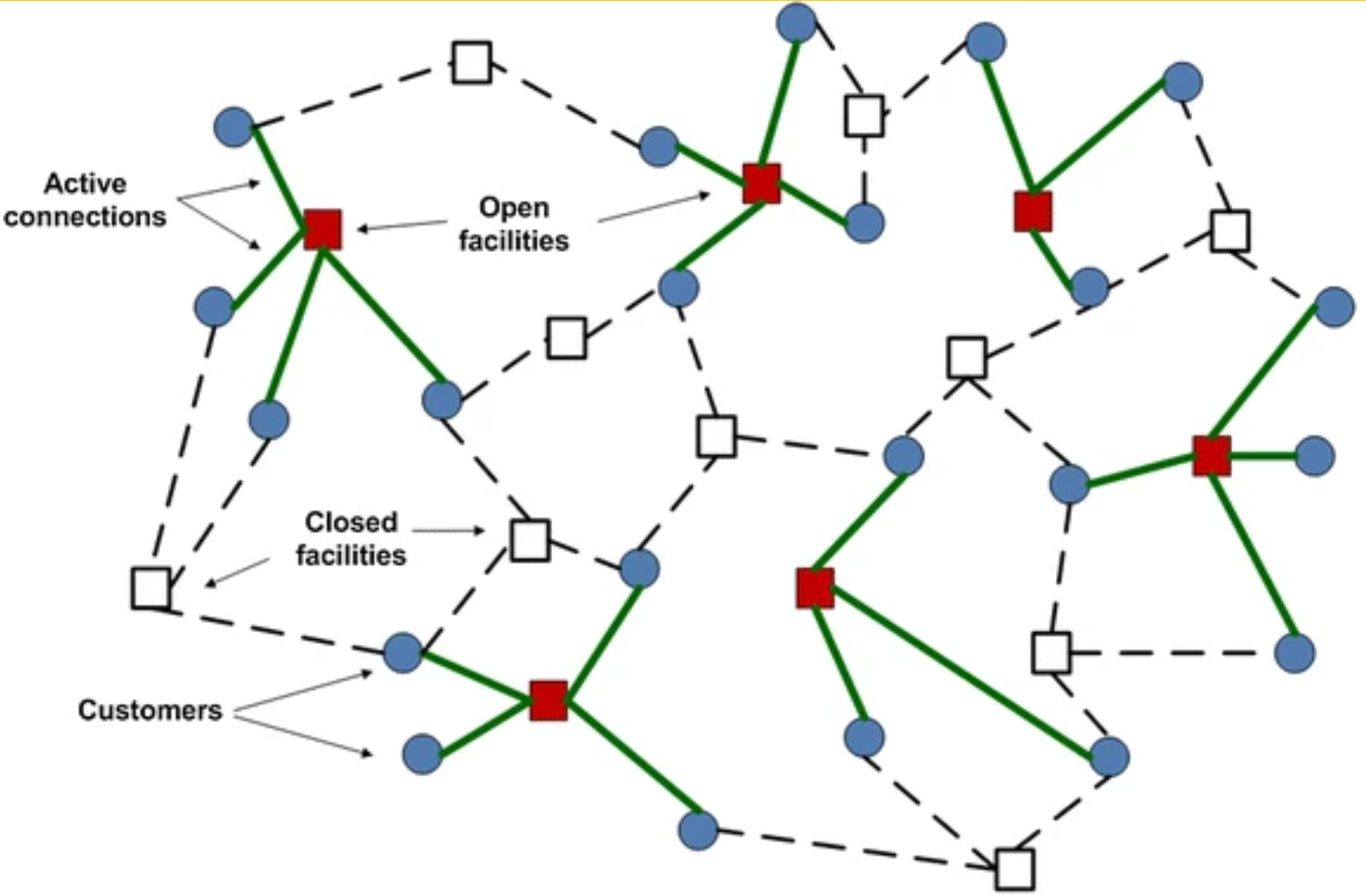
  • Facility location problems: In this problem, the objective is to determine the optimal location for new facilities based on factors such as distance to customers, transportation costs, and capacity requirements. It has applications in urban planning, supply chain management, and network design.

  • Graph matching: Graph matching problems involve finding the optimal correspondence or alignment between two or more graphs. This is often applied in image recognition, pattern recognition, or DNA sequence alignment.

These examples highlight the broad range of applications and complexity involved in combinatorial optimization, making it an important area of study within computer science.

The Optimization Lab at Math Faculty and many publications of the members are related to this topic.

(Amintoosi & Kohan-Baghkheirati, 2023; امین‌طوسی محمود & عزتی هاشم, 2020; Ezzati et al., 2021; Monsefi & Amintoosi, 2002; Amintoosi et al., 2004; Amintoosi et al., 2004; Amintoosi & Haddadnnia, 2005; Amintoosi et al., 2007; Amintoosi et al., 2007; منصفی ر. & امین‌طوسی م., 2000; امین‌طوسی م., 2000; امین‌طوسی م. & صدوقی‌یزدی ه., 2004; عزتی هاشم & امین‌طوسی محمود, 1398; Hokmabadi et al., 1396; عزتی هاشم et al., 1396; شاهی سمیرا et al., 1393; حسینی فاطمه‌سادات & امین‌طوسی محمود, 1393; رضازاده معصومه et al., 1393)

References

2023

  1. Amintoosi2023FS-bio-math.png
    Feature Selection for Anti-Cancer Plant Recommendation
    Mahmood Amintoosi, and Eisa Kohan-Baghkheirati
    In The 2nd International and 4th National Conference on Biomathematics, Feb 2023
    PDF Code

2021

  1. Ezzati99.jpg
    On the Minimum of True Matches in Exact Graph Matching with Simulated Annealing
    Hashem Ezzati, Mahmood Amintoosi, and Hashem Tabasi
    Journal of Algorithms and Computation, Feb 2021
    HTML PDF

2020

  1. ModifiedGA-iranaict99.jpg
    الگوریتم ژنتیکِ آگاه از بهترین عضو با کاربرد در رنگ‌آمیزی و بعدمتریک گراف
    محمود امین‌طوسی, and هاشم عزتی
    نشریه فناوری اطلاعات و ارتباطات ایران, Feb 2020
    The aware genetic algorithm of the best member, applied to graph coloring and metric-dimension of the graph problem
    HTML PDF

2019

  1. Ezzati98-TSCO-GD.png
    محاسبه بعد متریک گراف با الگوریتم شبیه‌سازی تبریدی
    هاشم عزتی, and محمود امین‌طوسی
    In سومین سمینار کنترل و بهینه‌سازی, Feb 2019
    Computing Graph Metric Dimension using Simulated Annealing
    PDF

2017

  1. Hokmabadi96Coco.png
    Solving uncapacitated facility location problem by cuckoo optimization algorithm
    Somayye Hokmabadi, Mahmood Amintoosi, and Mohammad Ali Partanian
    In 48th Annual Iranian Mathematics Conference, Feb 2017
    PDF
  2. Ezzati96graph.png
    یک حد بالا برای حداقل تعداد تطابقات درست در مسئله تطابق گراف با روش‌های مبتنی بر جستجوی تصادفی
    هاشم عزتی, محمود امین‌طوسی, and هاشم طبسی
    In چهل و هشتمین کنفرانس ریاضی ایران, Feb 2017
    An Upper Bound for Minimum True Matches in Graph Isomorphism with Stochastic Methods
    PDF

2014

  1. UFL.png
    مقایسه سه روش فراابتکاری در حل UFLP
    سمیرا شاهی, محمود امین‌طوسی, and مهدی زعفرانیه
    In هفتمین کنفرانس بین‌المللی انجمن ایرانی تحقیق در عملیات, Feb 2014
    Comparing 3 meta-heuristic methods for solving UFLP
    PDF
  2. Hoseini93mincutSA.png
    برش کمینه‌ی گراف با شبیه‌سازی تبریدی
    فاطمه‌سادات حسینی, and محمود امین‌طوسی
    In هفتمین کنفرانس بین‌المللی انجمن ایرانی تحقیق در عملیات, Feb 2014
    Graph Minumum Cut using SA
    PDF
  3. IMS.png
    مسئله مکان‌یابی p -هاب با ظرفیت نامتناهی در حضور صف M/G/1
    معصومه رضازاده, محمود امین‌طوسی, and مهدی زعفرانیه
    In چهل و پنجمین کنفرانس ریاضی ایران, Feb 2014
    Facility Location Problem in M/G/1 Queue
    PDF

2007

  1. tiling.png
    Using Pattern Matching for Tiling and Packing Problems
    M. Amintoosi, H. SadoghiYazdi,  M.Fathy, and 1 more author
    European Journal of Operational Research, Feb 2007
    Indexed by DBLP and SCOPUS
    PDF
  2. fish-school.jpg
    A Fish School Clustering Algorithm: Applied to Student Sectioning Problem
    M. Amintoosi, M. Fathy, N. Mozayani, and 1 more author
    Dynamics of Continuous Discrete & Impulse Systems, series B: Applications and Algorithms, Dec 2007
    Post Proceeding of LSMS2007, Life System Modeling and Simulation 2007, China
    PDF

2005

  1. pubs.png
    Feature Selection in A Fuzzy Student Sectioning Algorithm
    M. Amintoosi, and J. Haddadnnia
    Lecture Notes in Computer Science, Dec 2005
    Indexed by DBLP
    PDF

2004

  1. pubs.png
    Fuzzy Student Sectioning
    M. Amintoosi, H. Sadoghi Yazdi, and J. Haddadnnia
    In PATAT04: Practice and Theory of Automated Timetabling, Aug 2004
  2. pubs.png
    Using Pattern Matching for Tiling and Packing Problems
    M. Amintoosi, R. Monsefi, and J. Haddadnia
    In Fifth International Conference on Computer Sciences, Jul 2004
  3. pubs.png
    کلاسه‌بندی فازی بهینه دانشجویان با استفاده از یک تابع فازی در حل مسئله برنامه‌ریزی ژنتیکی دروس هفتگی دانشگاه
    م. امین‌طوسی, and ه. صدوقی‌یزدی
    In نهمین كنفرانس سالانه انجمن كامپیوتر ایران, اسفند 2004
    Student’s sectioning using fuzzy inference system
    PDF

2002

  1. Pentomino_Puzzle_Solution_8x8_Minus_Center.svg.png
    A Genetic-Neuro Algorithm for Tiling Problems with Rotation and Reflection of Figures
    R. Monsefi, and M. Amintoosi
    Iranian Journal of Science and Technology, Transaction B, Dec 2002
    Indexed by ACM
    PDF

2000

  1. tiling.png
    جورچینی قطعات راست گوشه با استفاده از شبكه های عصبی و الگوریتم ژنتیك
    ر. منصفی, and م. امین‌طوسی
    In پنجمین کنفرانس سالانه انجمن کامپیوتر ایران, بهمن 2000
    Tiling Problem using Neural Networks and Genetic Algorithm
  2. pubs.png
    مروری بر مسائل NP-Hard و NP-Complete
    م. امین‌طوسی
    In مجله‌ صفر و یک , بهار 2000
    شماره سوم, A review on NP-Hard and NP-Complete Problems
    PDF